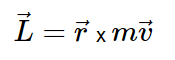Entering the Physics involved in the operation of the catapult, we have the torque, the force responsible for the circular movement that generates the launch of the projectile. Torque is a force that can cause an object to rotate around an axis, so that it takes on an angular acceleration and a rotational motion is initiated. Associated with this movement, there is a physical quantity called Moment of Inertia, which can be characterized as a resistance to change in rotational motion.
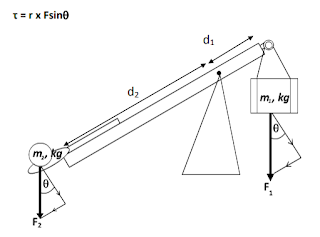
Figure 3. Schematic of forces acting on the trebuchet arm.
LUCAS, Stephen, HORNERS, Salters. What affects the range of a trebuchet
Observing the anatomy of the catapult, one can notice the application of the aforementioned concept, the torque, at both ends of his arm.
As the counterweight falls, the rotating arm describes a circular trajectory, with tangential velocity (1), equivalent to the multiplication of the radius of that arm by the angular velocity found.
But to find the value of this angular velocity, you must first calculate
the torque (2), as it will help us find the angular acceleration, which
will complement the angular velocity formula.
In the above equation, we have "r" as the perpendicular distance from the end of the analyzed arm to the center of rotation, and the "F" as the applied force.
However, in order to find the torque, it must first be observed that the force vector forms an angle with the arm of the projectile and the counterweight, so the weight must be multiplied by the sine of that angle, according to the given formula.
Figure 4. Torque on the edges of the arm.
LUCAS, Stephen, HORNERS, Salters. What affects the range of a trebuchet?
The problem is that this angle is small and very difficult to measure, so during calculations it is considered negligible. Therefore, in order to find the resulting torque, the existence of this angle is neglected, and considers the torque of the arm with the highest weight with positive direction and the torque of the smaller, negative arm, as shown in the formula below.
A new equation will be used after finding the value of the resulting torque, where this value will be applied to find other components needed for the calculations. This new equation, defined below, relates angular acceleration to torque, since both are inherently interconnected.
In the equation above, a relation is also made with the moment of inertia (5), which as explained earlier, is the force that "slows" a rotational movement, therefore it is a resistance force. Consequently, if there is a force that is contrary to the movement, its acceleration will be influenced.
The formula above can be used in several situations, such as in a system with several point masses, but in the case of trebuchet, only the masses of the projectile and the counterweight will be considered. The equation considers "r" to be the distance from the center of mass to the axis of rotation and "m" the mass analyzed.
Finally, when calculating the values of the resulting torque
and the moment of inertia, it will be possible to find the angular
acceleration. The same can be applied in the torricelli equation of angular
velocity, as shown below:
In this equation, the initial omega should be considered
zero, since the catapult's arm starts from rest and the value of
"theta" as the angular displacement of the arm, that is, the angle of
the place from which it departed with the position in which the projectile is
released.
Figure 5. Angle of the launching arm of the catapult.
LUCAS, Stephen, HORNERS, Salters. What affects the range of a trebuchet?
From this value found for angular velocity, it will be possible to transform it into linear by a small conversion, by the equation (1). This linear velocity will be the launch velocity of the projectile, which will make possible finding the value of the range described by the equation (8) where "V" is the linear velocity which the projectile leaves the catapult.
The trajectory of the projectile is described by the figure 7 and will be the angle indicated which will determine the movement.
Figure 7. Angle of the launching arm of the catapult.
LUCAS, Stephen, HORNERS, Salters. What affects the range of a trebuchet?
Proof of the best launch angle
Regarding the oblique launch, there is a variety of angles of which a projectile can be cast. However there is an angle that is proven to be the most far-reaching one, which is the 45° angle. Neglecting the resistance of the air, it will be proved below the theory behind this statement.
Figure 8. Proof of the best launch angle.
The conversion of Potential Energy into Kinetics
The first law of thermodynamics says that the state of energy can not be created or destroyed, only converted, therefore energy is always conserved. Before the projectile is fired, the counterweight is suspended at a certain height from the ground, which generates a gravitational potential energy, determined by the formula:
When an object falls, its gravitational potential energy is transformed into kinetic energy. Consequently, considering that all potential gravitational energy is transformed into kinetic energy, we have:
.
Below we have an image that illustrates the idea of the transformation of gravitational potential energy into kinetic:
Figure 9. Gravitational potential energy and Kinetic.
Conservation of Angular Momentum
Amount of motion and angular momentum are very close concepts. The first is about every body that is in motion while the second is the exact same, except that the movement generated is that of rotation.
Angular momentum is related to the tendency of the body to continue its state of circular motion. Thus, it is a vector perpendicular to the amount of motion associated with a body in rotational motion around a fixed point.
Figure 10. Angular momentum.
Where L is given by the following equation:
In this formula, the radius vector is related between the object and the axis of rotation, the mass of the object and the velocity vector of the object.
Using the formula in figure 5, it is possible to convert this linear velocity into angular and substitute in the above equation, with the following formula:

 .
.
When we speak of bodies in a circular motion, we can relate their mass distribution in the body and how this distribution relates to the radius of movement. This quantity is called the moment of inertia, given by equation (5). Therefore, we can rewrite the angular momentum equation as follows:
3D Model
Figure 11. 3D Model of the Catapult
Source: Own
Technical Views
Figure 12. Technical views of the Catapult
Bibliography
LUCAS, Stephen, HORNERS, Salters. What affects the range of a trebuchet?.
HALLIDAY D.; RESNICK R. e WALKER J. Fundamentos de Física: mecânica. Volume 1. 8ª edição. Editora
LTC, 2009.
RAMACIOTTI, André. Ataleia. Available in:< https://aleteia.wordpress.com/2009/04/06/lancamento
s-obliquos-alcance-maximo/.
Torque. Khanacademy. Available in:< https://pt.khanacademy.org/science/physics/torque-angular-momentum>.
Catapulta Trebuchet. Canstockphoto. Available in: <https://www.canstockphoto.com.br/catapulta-antiga-tiro-medieval-51216994.html>.